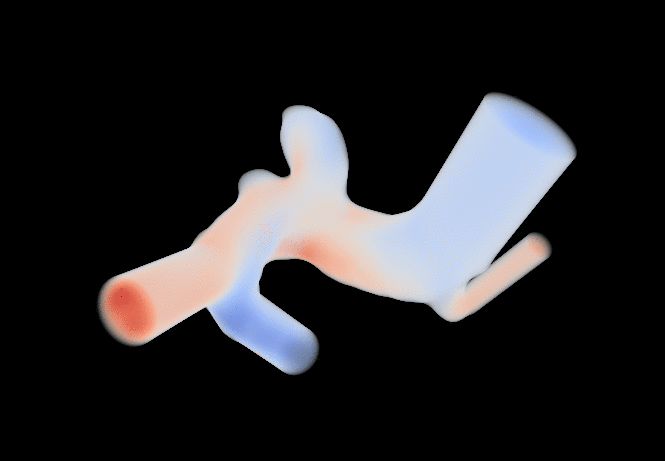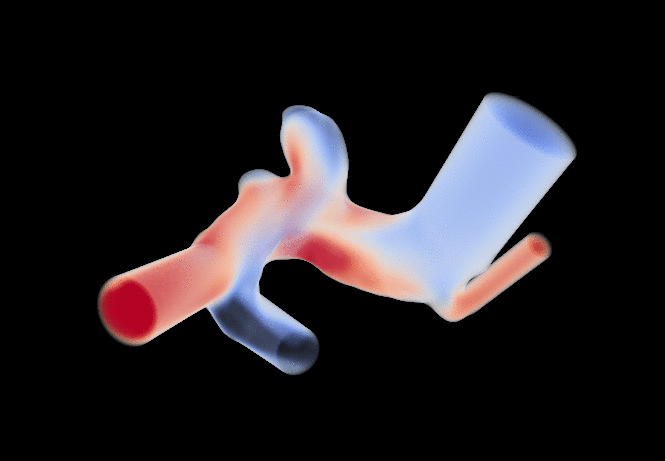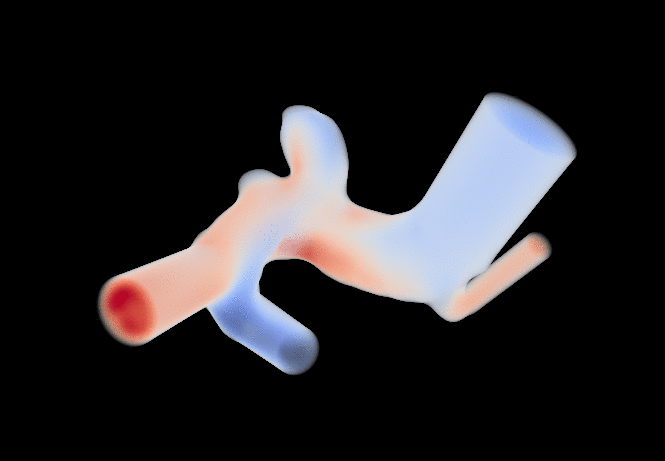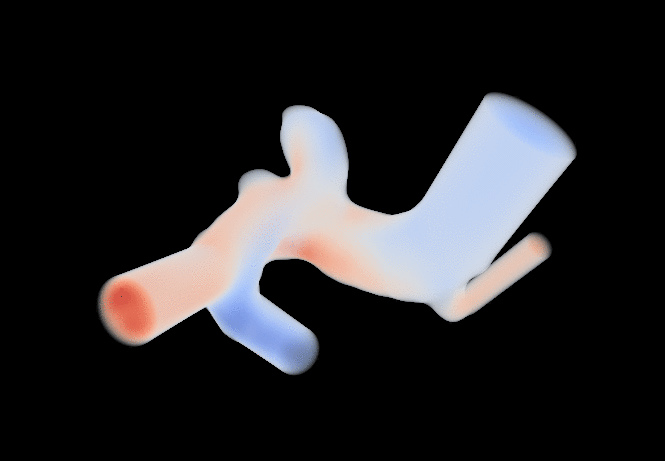
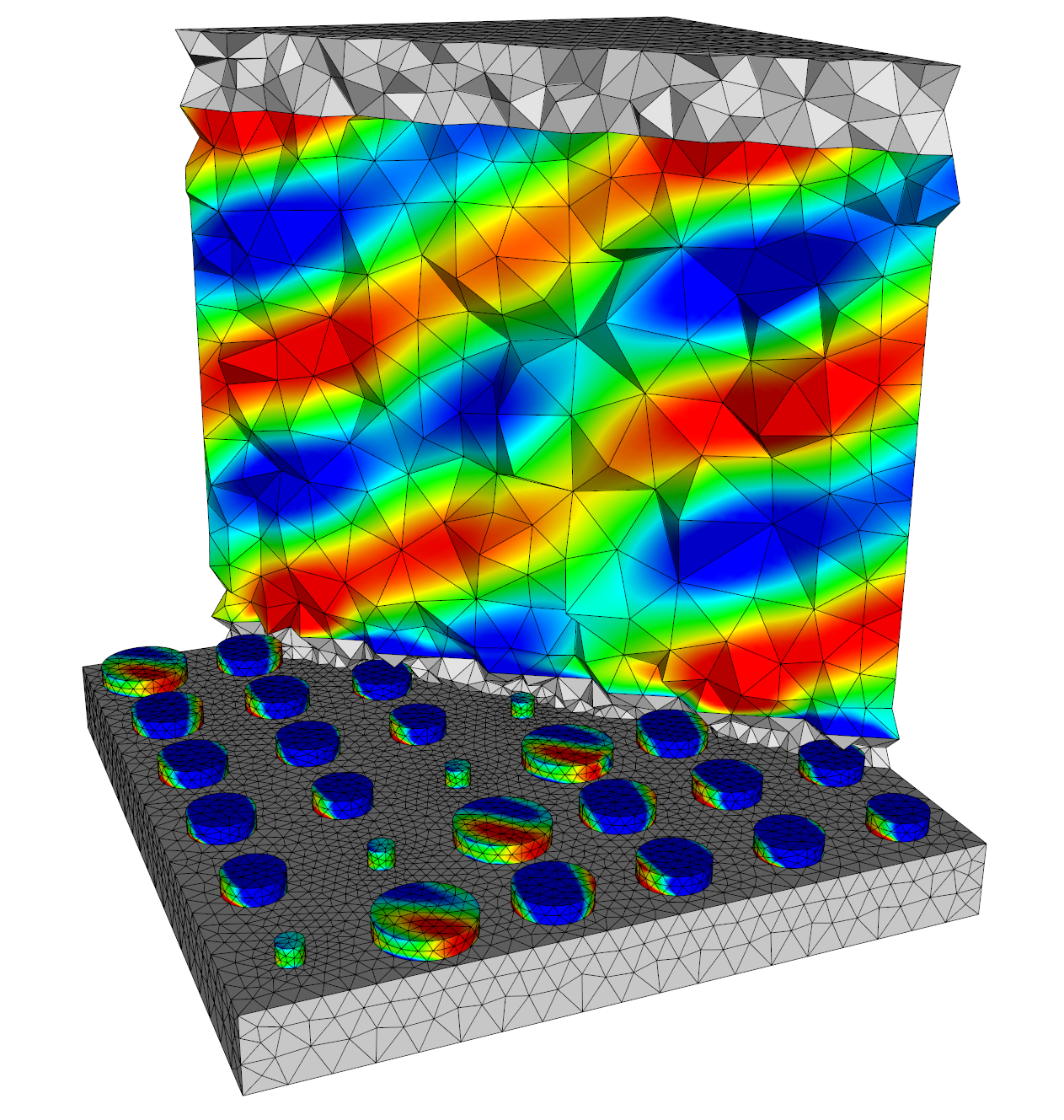
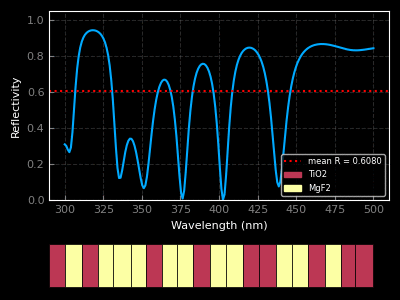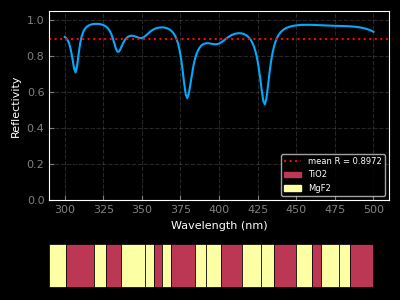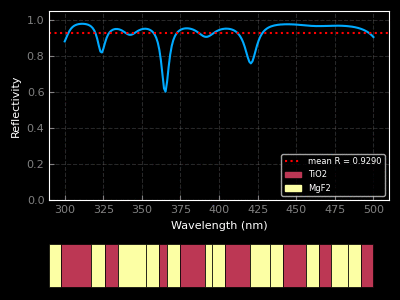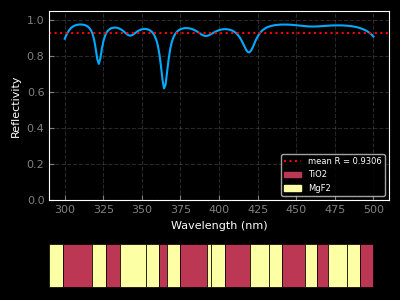
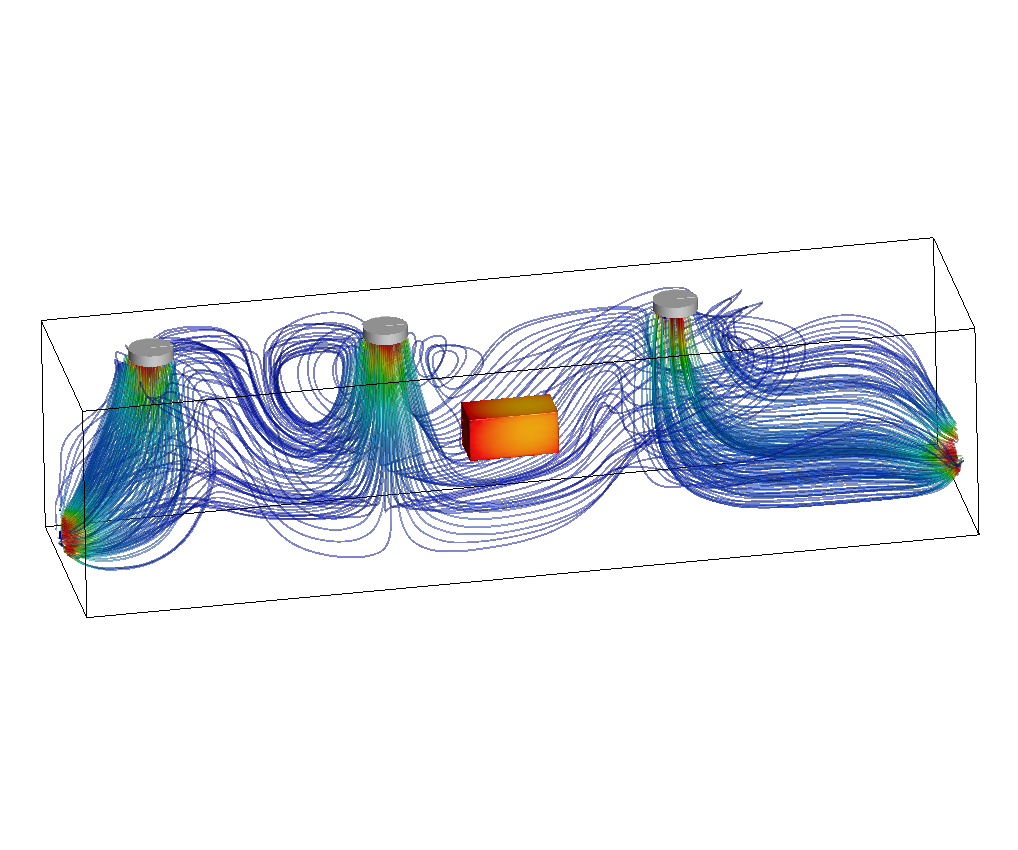
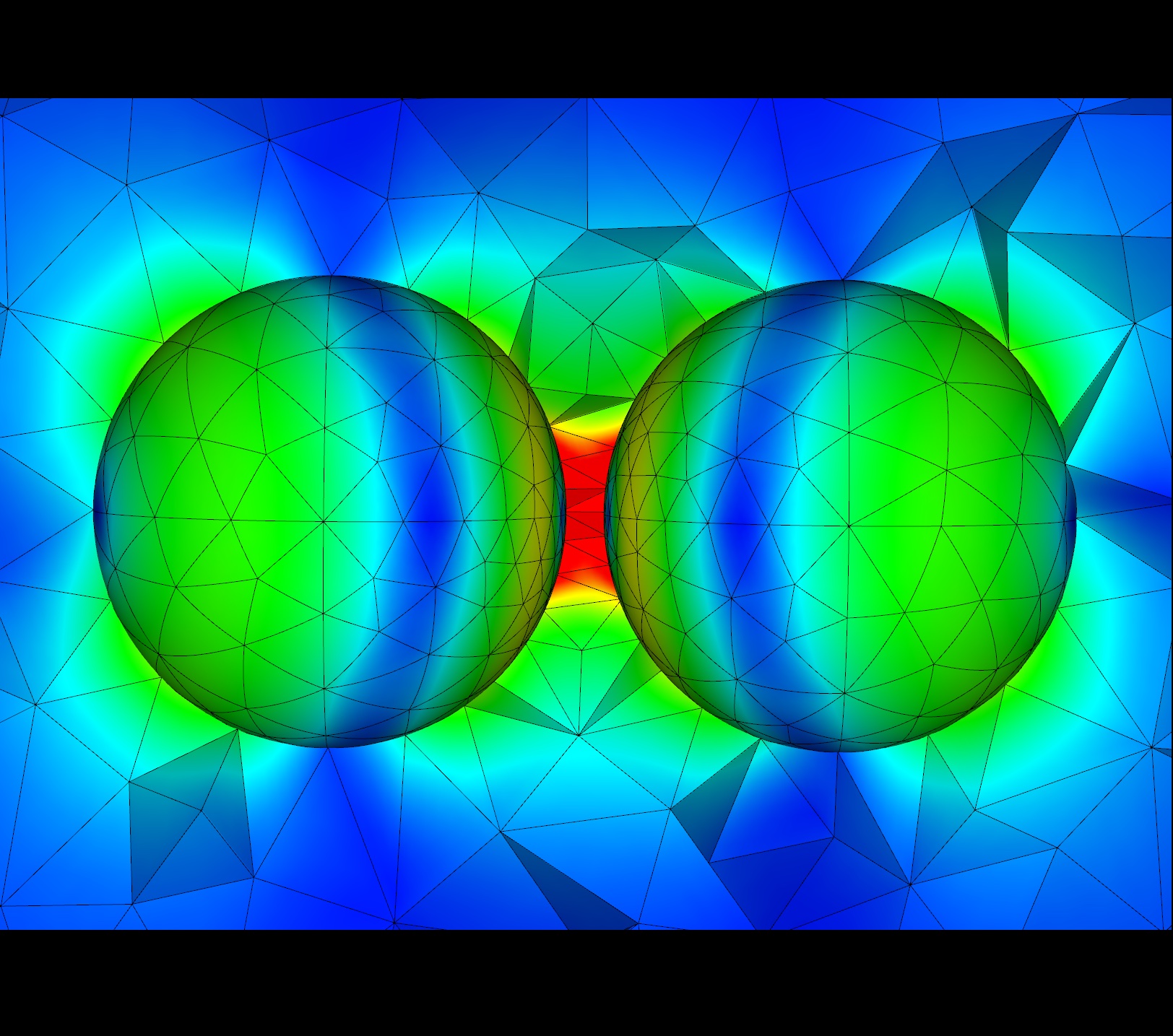
I am currently a research engineer in the CFL team at CEMEF, Sophia-Antipolis. My current work is concerned with the application of machine learning algorithms to CFD problems (see the MINDS project). Find out more about what I do below or by downloading my résumé. You can also find a list of the publications I was associated to here.